Understanding The Dirac Delta Function: A Comprehensive Guide

The Dirac delta function is a fundamental concept in mathematics and physics, particularly in the fields of signal processing, quantum mechanics, and systems theory. This unique function serves as a powerful tool for modeling and analyzing systems with impulse responses and point sources. In this article, we will dive deep into the intricacies of the Dirac delta function, exploring its properties, applications, and significance in various scientific domains.

As we embark on this journey, we will unravel the mysteries surrounding the Dirac delta function, demonstrating its relevance through practical examples and mathematical formulations. Our goal is to provide you with a comprehensive understanding that will enhance your knowledge and appreciation of this remarkable mathematical entity.

Whether you are a student, educator, or professional in the fields of engineering or physics, this article aims to equip you with the insights needed to effectively utilize the Dirac delta function in your work. Let’s begin our exploration of this fascinating mathematical concept!

Table of Contents

• What is the Dirac Delta Function?
• Properties of the Dirac Delta Function
• Mathematical Definition
• Applications in Physics
• Signal Processing Applications
• Connection to Other Functions
• Common Misconceptions
• Conclusion

What is the Dirac Delta Function?

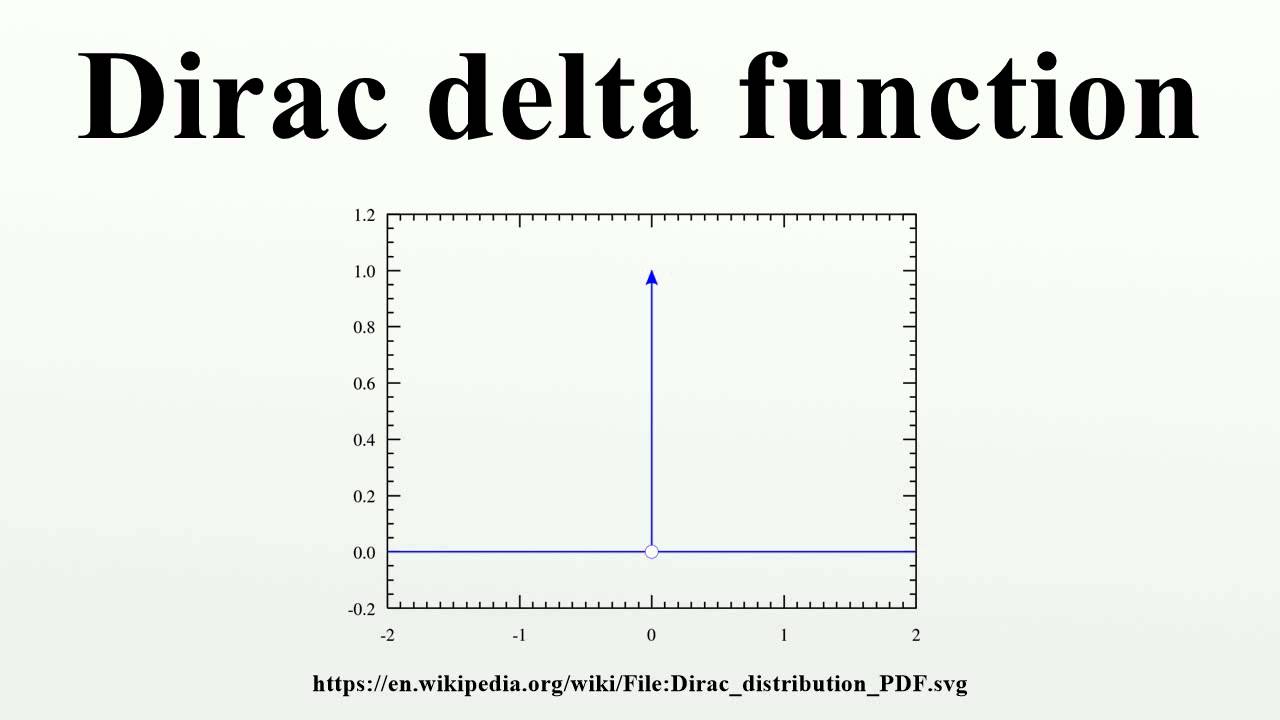
The Dirac delta function, often denoted as δ(x), is not a function in the traditional sense but rather a distribution or generalized function. It is defined to have the following properties:

• δ(x) = 0 for all x ≠ 0
• ∫ δ(x) dx = 1, for the integral over the entire real line

This unique behavior allows the Dirac delta function to act as an idealized representation of a point source or an impulse. It is commonly used in various mathematical and engineering applications where such idealized conditions are useful.

Properties of the Dirac Delta Function

The Dirac delta function possesses several important properties that make it a versatile tool in mathematical analysis:

1. Sifting Property

The sifting property states that for any continuous function f(x), the following holds:

∫ f(x) δ(x - a) dx = f(a)

This property allows the Dirac delta function to "sift out" the value of the function at a specific point.

2. Scaling Property

The scaling property indicates how the Dirac delta function behaves under scaling transformations:

δ(ax) = (1/|a|) δ(x)

for a ≠ 0. This property is essential when working with transformations in analysis.

3. Shifting Property

The shifting property describes how the Dirac delta function can be translated along the x-axis:

δ(x - a) = 0 for x ≠ a

This property is useful in applications involving shifted impulse responses.

Mathematical Definition

The mathematical definition of the Dirac delta function can be understood through its representation as a limit of functions. A common representation is:

δ(x) = lim (ε → 0) (1/(π(1 + x²/ε²)))

This formulation illustrates how the Dirac delta function can be approximated by a family of functions that become increasingly peaked as ε approaches zero.

Applications in Physics

The Dirac delta function finds numerous applications in physics, especially in areas such as quantum mechanics and electromagnetism:

• Quantum Mechanics: In quantum mechanics, the Dirac delta function is used to represent point particles and their interactions. It helps to express wave functions and probability distributions.
• Electromagnetism: The delta function is utilized in the formulation of charge distributions and in the analysis of electric fields generated by point charges.

Signal Processing Applications

In signal processing, the Dirac delta function is essential for modeling systems and analyzing signals. Here are some of its key applications:

• Impulse Response: The impulse response of a system can be represented using the Dirac delta function, allowing engineers to analyze the output of a system when subjected to a point input.
• Convolution: The convolution operation, which is fundamental in signal processing, heavily relies on the properties of the Dirac delta function to simplify calculations.

Connection to Other Functions

The Dirac delta function is closely related to other mathematical functions:

• Heaviside Step Function: The Heaviside step function is defined as the integral of the Dirac delta function.
• Gaussian Function: The Gaussian function can approximate the Dirac delta function as its variance approaches zero.

Common Misconceptions

Despite its widespread use, several misconceptions exist regarding the Dirac delta function:

• Some people mistakenly believe that the Dirac delta function is a traditional function; it is, in fact, a distribution.
• Another common misconception is that the Dirac delta function can take non-zero values; it is only defined at the point of singularity.

Conclusion

In this comprehensive guide, we have explored the Dirac delta function, its properties, applications, and significance across various scientific domains. This unique mathematical entity proves to be an indispensable tool in both theoretical and applied contexts.

As you continue your journey into the realms of mathematics and physics, consider the many ways in which the Dirac delta function can enhance your understanding and problem-solving abilities. We encourage you to leave your thoughts in the comments below, share this article with others, or explore additional resources on our site to further expand your knowledge!

References

• Rudin, W. (1976). Principles of Mathematical Analysis. New York: McGraw-Hill.
• Gelfand, I. M., & Shilov, G. E. (1964). Generalized Functions, Vol. 1. Academic Press.
• Strang, G. (1993). Introduction to Linear Algebra. Wellesley-Cambridge Press.