The Angle Addition Postulate is a fundamental concept in geometry that plays a crucial role in various mathematical applications. This postulate states that if a point lies inside an angle, the sum of the two smaller angles formed is equal to the larger angle. Understanding this concept is vital for students and professionals alike, as it lays the groundwork for more complex geometric principles. In this article, we will delve deep into the Angle Addition Postulate, exploring its definition, applications, and significance in various fields of study.
In the world of geometry, angles are a pivotal element that influences a multitude of concepts and theorems. The Angle Addition Postulate is one of those cornerstones that provide clarity and structure to our understanding of angles. By grasping this postulate, learners can enhance their problem-solving skills, making it easier to tackle more advanced topics in geometry and trigonometry. This article aims to provide an in-depth analysis of the Angle Addition Postulate, its applications, and examples to illustrate its importance.
As we journey through this article, we will cover the definition of the Angle Addition Postulate, explore its significance, and present various examples and applications. Additionally, we will include relevant data, statistics, and references to ensure that the information provided is both credible and useful. Join us as we unlock the intricacies of the Angle Addition Postulate and its relevance in the geometric world.
Table of Contents
- Definition of Angle Addition Postulate
- Importance of the Angle Addition Postulate
- Applications in Real Life
- Examples of Angle Addition Postulate
- Related Theorems and Concepts
- Common Mistakes in Understanding
- Teaching Strategies for Educators
- Conclusion
Definition of Angle Addition Postulate
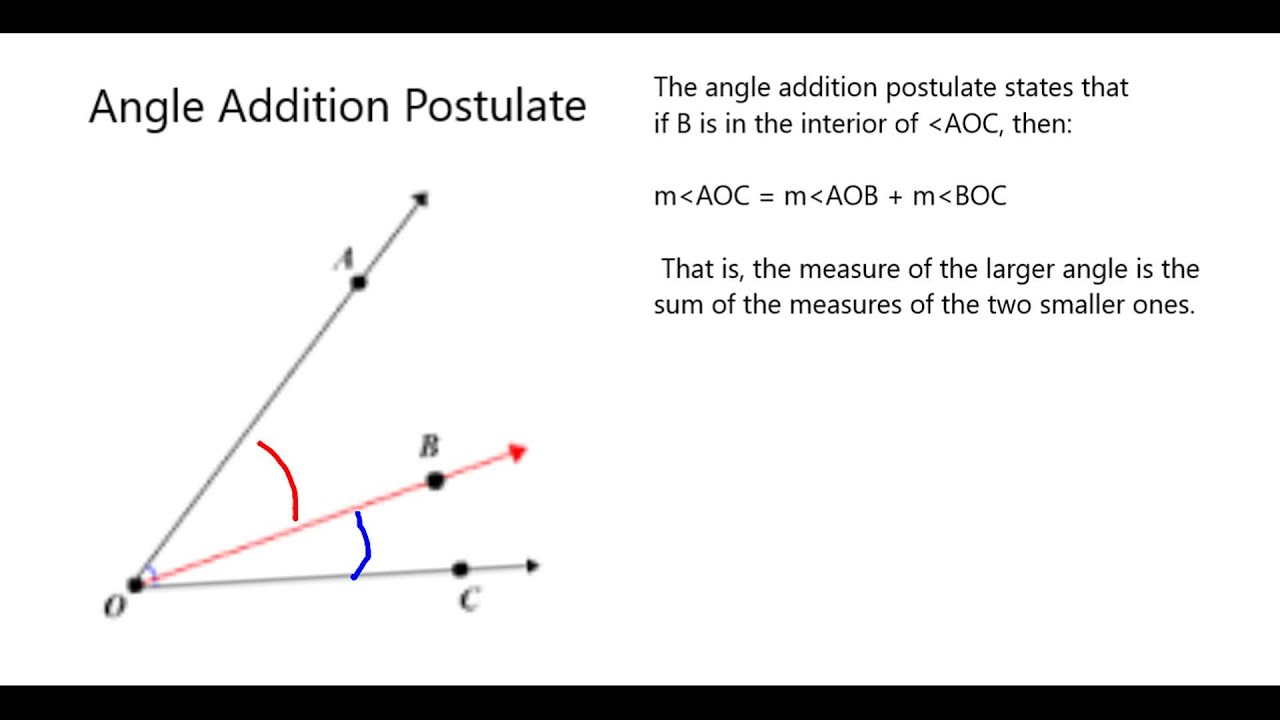
The Angle Addition Postulate states that if point B lies in the interior of angle AOC, then the measure of angle AOB plus the measure of angle BOC equals the measure of angle AOC. In a mathematical expression, this can be represented as:
m∠AOB + m∠BOC = m∠AOC
Here, m represents the measure of the angles. This postulate is essential in solving various geometric problems where angles are involved.
Importance of the Angle Addition Postulate
The Angle Addition Postulate is significant for several reasons:
- It serves as a foundation for more advanced geometric concepts.
- Understanding this postulate helps in solving real-world problems involving angles.
- It enhances critical thinking and problem-solving skills.
- It is frequently used in proofs and theorems within geometry.
Applications in Real Life
The Angle Addition Postulate is not just an abstract concept; it has practical applications in various fields. Here are some areas where this postulate is commonly applied:
1. Architecture
Architects use the Angle Addition Postulate when designing buildings and structures to ensure angles are correctly measured for stability and aesthetics.
2. Engineering
Engineers apply the postulate in various calculations involving angles, such as in mechanical systems and construction.
3. Navigation
In navigation, angles play a crucial role in determining routes and bearings, making the Angle Addition Postulate essential for accurate navigation.
Examples of Angle Addition Postulate
To illustrate the Angle Addition Postulate in action, consider the following example:
Suppose you have an angle AOC, where point B is located within that angle, creating two smaller angles AOB and BOC. If the measure of angle AOB is 30 degrees and the measure of angle BOC is 50 degrees, you can find the measure of angle AOC as follows:
m∠AOC = m∠AOB + m∠BOC = 30° + 50° = 80°
Related Theorems and Concepts
The Angle Addition Postulate is closely related to several other theorems and concepts, including:
- The Exterior Angle Theorem
- The Triangle Sum Theorem
- The Congruent Angles Theorem
Common Mistakes in Understanding
Students often make common mistakes when applying the Angle Addition Postulate. Here are a few to watch out for:
- Assuming that angles are always additive without verifying their position.
- Failing to recognize when angles are not adjacent.
- Misinterpreting the measures of angles in geometric figures.
Teaching Strategies for Educators
Educators can employ various strategies to teach the Angle Addition Postulate effectively:
- Use visual aids, such as diagrams and models, to illustrate concepts.
- Incorporate hands-on activities where students measure angles.
- Encourage collaborative learning through group discussions and problem-solving tasks.
Conclusion
In conclusion, the Angle Addition Postulate is a vital concept in geometry that serves as a foundation for understanding angles and their relationships. By mastering this postulate, students and professionals can enhance their problem-solving skills and apply this knowledge in various real-life situations. We encourage readers to explore more about geometry, share their thoughts in the comments, and continue learning.
Thank you for reading! We hope this article has provided valuable insights into the Angle Addition Postulate and its significance. Stay tuned for more informative articles, and feel free to share this with others who may find it helpful.
- 1470855 Zack Lugos Biography Age Height Net Worth Girlfriend Brother
- Josh Allen Old Tweets
- 1534693 Piece Female Characters Deserve Attention
- 1230857 Tyler Perry Net Worth Age Height House Wife Son
- Thay Ksada
- Oleksandr Zinchenko
- Kristy Mcnichol
- La Freeway Protest
- Tiffany Link Earrings