Understanding The Student's T Distribution: A Comprehensive Guide

The Student's T Distribution is a vital concept in statistics, particularly valuable when dealing with small sample sizes. This distribution plays a crucial role in hypothesis testing and in constructing confidence intervals. In this article, we will delve into the intricacies of the Student's T Distribution, exploring its definition, properties, applications, and significance in statistical analysis.

As we navigate through this guide, you will learn about the mathematical foundations of the Student's T Distribution, its practical applications in real-world scenarios, and how it compares to the normal distribution. Whether you are a student, researcher, or professional statistician, understanding the T distribution can enhance your analytical skills and help you make more informed decisions based on statistical data.

With an emphasis on expertise, authoritativeness, and trustworthiness, this article aims to provide you with a thorough understanding of the topic. By the end of our exploration, you will be equipped with the knowledge necessary to apply the Student's T Distribution in your work, from academic research to industry applications.

1. What is the Student's T Distribution?
2. Properties of the Student's T Distribution
3. Applications of the Student's T Distribution
4. T Distribution vs. Normal Distribution
5. Calculating T Scores
6. Confidence Intervals and Hypothesis Testing
7. Common Misconceptions about the T Distribution
8. Conclusion

1. What is the Student's T Distribution?

The Student's T Distribution, often simply referred to as the T Distribution, is a type of probability distribution that is symmetrical and bell-shaped, similar to the normal distribution. However, it has heavier tails, which means it is more prone to producing values that fall far from its mean.

This distribution was first described by William Sealy Gosset in 1908 under the pseudonym "Student." It was developed to address the challenges of estimating population parameters when sample sizes are small, typically less than 30. The T Distribution is particularly useful in situations where the population standard deviation is unknown, and it accounts for the increased variability that comes from small sample sizes.

The T Distribution is defined by its degrees of freedom (df), which are calculated as the sample size minus one (n - 1). As the sample size increases, the T Distribution approaches the normal distribution, making it a versatile tool for statisticians.

2. Properties of the Student's T Distribution

The Student's T Distribution has several key properties that distinguish it from other distributions:

Symmetry: The T Distribution is symmetrical around its mean, which is zero.
Heavier Tails: Compared to the normal distribution, the T Distribution has heavier tails, providing a better estimate for the variability in small samples.
Degrees of Freedom: The shape of the T Distribution depends on the degrees of freedom; as df increases, the distribution approaches the normal distribution.
Mean and Variance: The mean of the T Distribution is zero, while its variance is greater than one (specifically, it is df/(df - 2) for df > 2).

3. Applications of the Student's T Distribution

The Student's T Distribution is widely used in various fields, including:

Hypothesis Testing: The T Distribution is applied in t-tests to determine if there are significant differences between means.
Confidence Intervals: It is used to construct confidence intervals for population means, especially when the sample size is small.
Regression Analysis: The T Distribution is utilized to assess the significance of coefficients in regression models.
Quality Control: Industries use the T Distribution to analyze small samples for quality assurance purposes.

4. T Distribution vs. Normal Distribution

Understanding the differences between the T Distribution and the normal distribution is crucial for proper statistical analysis:

Sample Size: The T Distribution is preferred for small sample sizes, while the normal distribution is used for larger samples.
Shape: The T Distribution has heavier tails, which means it accounts for more extreme values than the normal distribution.
Convergence: As the sample size increases, the T Distribution approaches the normal distribution, making them similar under large sample conditions.

5. Calculating T Scores

To calculate the T score, you can use the following formula:

T = (X̄ - μ) / (s / √n)

Where:

X̄: Sample mean
μ: Population mean
s: Sample standard deviation
n: Sample size

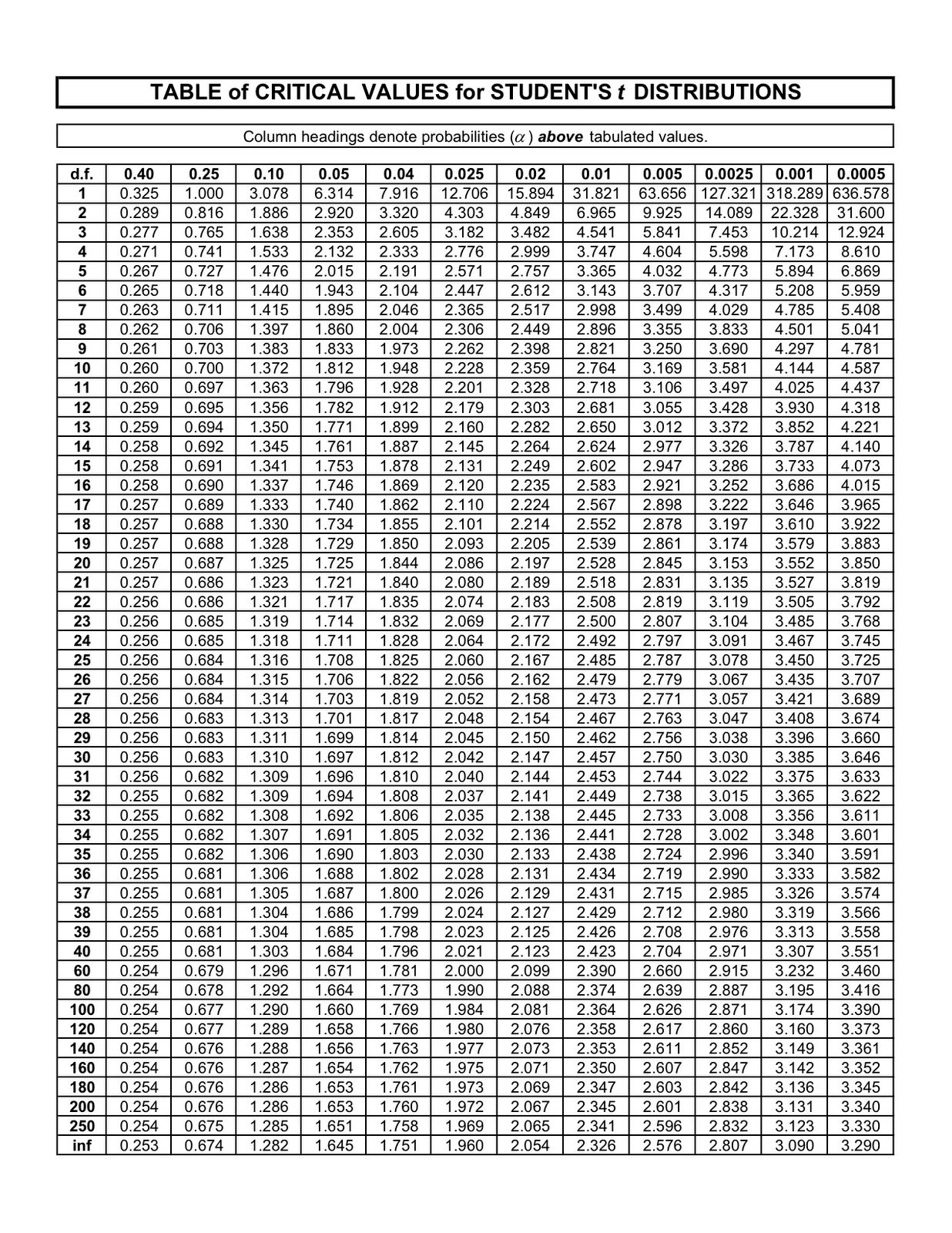
Once calculated, the T score can be compared against critical values from the T Distribution table based on the desired significance level and degrees of freedom.

6. Confidence Intervals and Hypothesis Testing

When using the T Distribution, constructing confidence intervals and performing hypothesis testing are essential statistical procedures:

Confidence Intervals: The formula for a confidence interval for the mean is:

CI = X̄ ± (t * (s / √n))

Hypothesis Testing: To conduct a t-test, you compare the calculated T score to the critical T value from the T Distribution table to determine whether to reject the null hypothesis.

7. Common Misconceptions about the T Distribution

Several misconceptions about the Student's T Distribution can lead to statistical errors:

Only for Small Samples: While the T Distribution is primarily used for small samples, it can also be applied for larger samples when the population standard deviation is unknown.
Normal Distribution Assumption: Many believe that T tests require the underlying data to be normally distributed, but the tests are robust to violations of this assumption with sufficiently large samples.
Misunderstanding Degrees of Freedom: Some users overlook the importance of degrees of freedom in determining the shape of the T Distribution.

8. Conclusion

In summary, the Student's T Distribution is an essential tool in the field of statistics, especially for analyzing small sample sizes. Its unique properties, applications in hypothesis testing and confidence intervals, and differences from the normal distribution make it a valuable resource for researchers and professionals alike.

We encourage you to explore and apply the concepts discussed in this article to enhance your statistical analysis skills. Don't hesitate to leave a comment, share this article with others, or check out more resources on this topic.

Thank you for reading, and we hope to see you back on our site for more insightful articles!